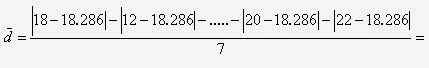Materia: PROBABILIDAD Y ESTADÍSTICA
Suponga que se
encuentra al final de una línea de ensamble final de un producto y que un supervisor
le ordena contar los elementos de un lote que se ha manufacturado hace unas
horas y del que se desconoce el número de productos que lo constituyen, de
inmediato usted empezará a contar un producto tras otro y al final informará al
supervisor que son, 48, 54 u otro número cualquiera. Ahora suponga que ese
mismo supervisor le plantea la siguiente pregunta ¿cuántas muestras o grupos
será posible formar con los productos del lote, si las muestras o grupos a
formar son de ocho elementos cada una de ellas?
En el primer caso el
cuantificar los elementos del lote no presenta dificultad alguna para la
persona encargada de hacerlo, pero cuando se le hace el segundo planteamiento,
al tratar de formar las muestras o grupos de ocho elementos la persona encargada
empezará a tener dificultad para hacerlo, en casos como este es necesario hacer
uso de las técnicas de conteo para cuantificar los elementos del evento en
cuestión (el número de muestras posibles a formar de ocho elementos), luego,
¿qué son las técnicas de conteo?
Las técnicas de conteo
son aquellas que son usadas para enumerar eventos difíciles de cuantificar.
Ejemplos en los que
definitivamente haremos uso de las técnicas de conteo serían:
-¿Cuántas comisiones
pro limpieza del instituto se pueden formar si hay 150 alumnos que desean
ayudar en esta tarea y se desea formar comisiones de ocho alumnos?
-¿Cuántas
representaciones de alumnos pueden ser formadas a) si se desea que estas
consten solo de alumnos de Ingeniería Química?, b) se desea que el presidente
sea un químico?, c) se desea que el presidente y tesorero sean químicos? Para
todos los casos, se desea que las representaciones consten de once alumnos.
-¿Cuántas maneras
tiene una persona de seleccionar una lavadora, una batidora y dos licuadoras, si
encuentra en una tienda 8 modelos diferentes de lavadoras, 5 modelos diferentes
de batidoras y 7 modelos diferentes de licuadoras?
Se les denomina
técnicas de conteo a: las combinaciones, permutaciones y diagrama de árbol, las
que a continuación se explicarán y hay que destacar que éstas nos proporcionan
la información de todas las maneras posibles en que ocurre un evento
determinado.
Las bases para
entender el uso de las técnicas de conteo son el principio multiplicativo y el
aditivo, los que a continuación se definen y se hace uso de ellos.
B)
PRINCIPIO MULTIPLICATIVO.
Si se desea realizar
una actividad que consta de r pasos, en donde el primer paso de la actividad a
realizar puede ser llevado a cabo de N1 maneras o formas, el segundo
paso de N2 maneras o formas y el r-ésimo paso de Nr
maneras o formas, entonces esta actividad puede ser llevada a efecto de;
N1
x N2 x ..........x Nr maneras o formas
El principio
multiplicativo implica que cada uno de los pasos de la actividad deben ser
llevados a efecto, uno tras otro.
Ejercicios:
1) Una persona desea
construir su casa, para lo cuál considera que puede construir los cimientos de
su casa de cualquiera de dos maneras (concreto o block de cemento), mientras
que las paredes las puede hacer de adobe, adobón o ladrillo, el techo puede ser
de concreto o lámina galvanizada y por último los acabados los puede realizar
de una sola manera ¿cuántas maneras tiene esta persona de construir su casa?
El principio multiplicativo, el aditivo y las técnicas de conteo que
posteriormente se tratarán nos proporcionan todas las maneras o formas posibles
de como se puede llevar a cabo una actividad cualquiera.
2) ¿Cuántas placas
para automóvil pueden ser diseñadas si deben constar de tres letras seguidas de
cuatro números, si las letras deben ser tomadas del abecedario y los números de
entre los dígitos del 0 al 9?, a. Si es posible repetir letras y números, b. No
es posible repetir letras y números, c. Cuántas de las placas diseñadas en el
inciso b empiezan por la letra D y empiezan por el cero, d. Cuantas de las
placas diseñadas en el inciso b empiezan por la letra D seguida de la G.
3) ¿Cuántos números
telefónicos es posible diseñar, los que deben constar de seis dígitos tomados
del 0 al 9?, a. Considere que el cero no puede ir al inicio de los números y es
posible repetir dígitos, b. El cero no debe ir en la primera posición y no es
posible repetir dígitos, c. ¿Cuántos de los números telefónicos del inciso b empiezan
por el número siete?, d. ¿Cuántos de los números telefónicos del inciso b
forman un número impar?.
C) PRINCIPIO ADITIVO.
Si se desea llevar a
efecto una actividad, la cuál tiene formas alternativas para ser realizada,
donde la primera de esas alternativas puede ser realizada de M maneras o
formas, la segunda alternativa puede realizarse de N maneras o formas ..... y
la última de las alternativas puede ser realizada de W maneras o formas,
entonces esa actividad puede ser llevada a cabo de,
M + N + .........+ W maneras o
formas
Ejercicios:
1) Una persona desea
comprar una lavadora de ropa, para lo cuál ha pensado que puede seleccionar de
entre las marcas Whirpool, Easy y General Electric, cuando acude a hacer la
compra se encuentra que la lavadora de la marca W se presenta en dos tipos de
carga ( 8 u 11 kilogramos), en cuatro colores diferentes y puede ser automática
o semiautomática, mientras que la lavadora de la marca E, se presenta en tres
tipos de carga (8, 11 o 15 kilogramos), en dos colores diferentes y puede ser
automática o semiautomática y la lavadora de la marca GE, se presenta en solo
un tipo de carga, que es de 11 kilogramos, dos colores diferentes y solo hay
semiautomática. ¿Cuántas maneras tiene esta persona de comprar una lavadora?
2 ) Rafael Luna desea ir a las Vegas o a Disneylandia en las próximas
vacaciones de verano, para ir a las Vegas él tiene tres medios de transporte
para ir de Chihuahua al Paso Texas y dos medios de transporte para ir del Paso
a las Vegas, mientras que para ir del paso a Disneylandia él tiene cuatro
diferentes medios de transporte, a) ¿Cuántas maneras diferentes tiene Rafael de
ir a las Vegas o a Disneylandia?, b) ¿Cuántas maneras tiene Rafael de ir a las
Vegas o a Disneylandia en un viaje redondo, si no se regresa en el mismo medio
de transporte en que se fue?.
D) PERMUTACIONES.
Para entender lo que
son las permutaciones es necesario definir lo que es una combinación y lo que
es una permutación para establecer su diferencia y de esta manera entender
claramente cuando es posible utilizar una combinación y cuando utilizar una
permutación al momento de querer cuantificar los elementos de algún evento.
COMBINACIÓN Y
PERMUTACION.
COMBINACIÓN:
Es todo arreglo de
elementos en donde no nos interesa el lugar o posición que ocupa cada uno de
los elementos que constituyen dicho arreglo.
PERMUTACIÓN:
Es todo arreglo de
elementos en donde nos interesa el lugar o posición que ocupa cada uno de los
elementos que constituyen dicho arreglo.
Vídeo Diferencia entre Permutación y Combinación: https://www.youtube.com/watch?v=3fbcfTlLIck
Vídeo Diferencia entre Permutación y Combinación: https://www.youtube.com/watch?v=3fbcfTlLIck
Para ver de una manera
objetiva la diferencia entre una combinación y una permutación, plantearemos
cierta situación.
Suponga que un salón
de clase está constituido por 35 alumnos. a) El maestro desea que tres de los
alumnos lo ayuden en actividades tales como mantener el aula limpia o entregar
material a los alumnos cuando así sea necesario. b) El maestro desea que se
nombre a los representantes del salón (Presidente, Secretario y Tesorero).
Solución:
a) Suponga
que por unanimidad se ha elegido a Daniel, Arturo y a Rafael para limpiar el
aula o entregar material, (aunque pudieron haberse seleccionado a Rafael,
Daniel y a Enrique, o pudo haberse formado cualquier grupo de tres personas
para realizar las actividades mencionadas anteriormente).
¿Es importante el
orden como se selecciona a los elementos que forma el grupo de tres personas?
Reflexionando al
respecto nos damos cuenta de que el orden en este caso no tiene importancia,ya
que lo único que nos interesaría es el contenido de cada grupo, dicho de otra
forma, ¿quiénes están en el grupo? Por tanto, este ejemplo es una combinación,
quiere decir esto que las combinaciones nos permiten formar grupos o muestras
de elementos en donde lo único que nos interesa es el contenido de los mismos.
b) Suponga
que se han nombrado como representantes del salón a Daniel como Presidente, a
Arturo como secretario y a Rafael como tesorero, pero resulta que a alguien se
le ocurre hacer algunos cambios, los que se muestran a continuación:
CAMBIOS
PRESIDENTE:
|
Daniel
|
Arturo
|
Rafael
|
Daniel
|
SECRETARIO:
|
Arturo
|
Daniel
|
Daniel
|
Rafael
|
TESORERO:
|
Rafael
|
Rafael
|
Arturo
|
Arturo
|
Ahora tenemos cuatro arreglos, ¿se trata de la misma representación?
Creo que la respuesta sería no, ya que el cambio de función que se hace a
los integrantes de la representación original hace que definitivamente cada una
de las representaciones trabaje de manera diferente, ¿importa el orden de los
elementos en los arreglos?. La respuesta definitivamente sería sí, luego
entonces las representaciones antes definidas son diferentes ya que el orden o
la forma en que se asignan las funciones sí importa, por lo tanto es este caso
estamos tratando con permutaciones.
A continuación obtendremos las fórmulas de permutaciones y de combinaciones, pero antes hay que definir lo que es n! (ene factorial), ya que está involucrado en las fórmulas que se obtendrán y usarán para la resolución de problemas.
n!= al producto desde la unidad hasta el valor que ostenta n.
n!= 1 x 2 x 3 x 4 x...........x n
Ejem.
10!=1 x 2 x 3 x 4 x.........x 10=3,628,800
8!= 1 x 2 x 3 x 4 x.........x 8=40,320
6!=1 x 2 x 3 x 4 x..........x 6=720, etc., etc.
Video n! por calculadora:
https://www.youtube.com/watch?v=KbrzmSHgk0E
Video n! por calculadora:
https://www.youtube.com/watch?v=KbrzmSHgk0E
Obtención de fórmula de permutaciones.
Para hacer esto, partiremos de un ejemplo.
¿Cuántas maneras hay de asignar los cuatro primeros lugares de un
concurso de creatividad que se verifica en las instalaciones de nuestro
instituto, si hay 14 participantes?
Solución:
Haciendo uso del principio multiplicativo,
14x13x12x11 = 24,024 maneras de asignar los primeros tres lugares del
concurso
Esta solución se debe, a que al momento de asignar el primer lugar
tenemos a 14 posibles candidatos, una vez asignado ese lugar nos quedan 13
posibles candidatos para el segundo lugar, luego tendríamos 12 candidatos
posibles para el tercer lugar y por último tendríamos 11 candidatos posibles
para el cuarto lugar.
Luego si n es el total de participantes en el concurso y r es
el número de participantes que van a ser premiados, y partiendo de la expresión
anterior, entonces.
14x13x12x11= n x (n - 1) x (n - 2) x .......... x (n – r + 1)
si la expresión anterior es multiplicada por (n – r)! / (n – r)!,
entonces
= n x (n –1 ) x (n – 2) x ......... x (n – r + 1) (n – r)! / (n – r)!
= n!/ (n – r)!
Por tanto, la fórmula de permutaciones de r objetos tomados de entre n
objetos es:
nPr = n! .
( n – r ) !
Esta fórmula nos
permitirá obtener todos aquellos arreglos en donde el orden es importante y
solo se usen parte (r) de los n objetos con que se cuenta, además hay que hacer
notar que no se pueden repetir objetos dentro del arreglo, esto es, los n
objetos son todos diferentes.
Entonces, ¿qué fórmula
hay que usar para arreglos en donde se utilicen los n objetos con que se
cuenta?
Si en la fórmula
anterior se sustituye n en lugar de r, entonces.
nPn= n!/ (n –n)! = n!
/ 0! = n! / 1 = n!
Como 0! = 1 de acuerdo a demostración matemática, entonces
nPn=
n!
1) ¿Cuantas
representaciones diferentes serán posibles formar, si se desea que consten de
Presidente, Secretario, Tesorero, Primer Vocal y Segundo Vocal?, sí esta
representación puede ser formada de entre 25 miembros del sindicato de una
pequeña empresa.
2) a. ¿Cuántas maneras
diferentes hay de asignar las posiciones de salida de 8 autos que participan en
una carrera de fórmula uno? (Considere que las posiciones de salida de los
autos participantes en la carrera son dadas totalmente al azar) b. ¿Cuántas
maneras diferentes hay de asignar los primeros tres premios de esta carrera de
fórmula uno?
Solución: https://www.youtube.com/watch?v=wreLxYoocTk
3) ¿Cuántos
puntos de tres coordenadas ( x, y, z ), será posible generar con los dígitos 0,
1, 2, 4, 6 y 9?, Si, a. No es posible repetir dígitos, b. Es posible repetir
dígitos.
4) a.
¿Cuántas maneras hay de asignar las 5 posiciones de juego de un equipo de básquetbol,
si el equipo consta de 12 integrantes?, b. ¿Cuántas maneras hay de asignar las
posiciones de juego si una de ellas solo puede ser ocupada por Uriel José
Esparza?, c. ¿Cuántas maneras hay de que se ocupen las posiciones de juego si
es necesario que en una de ellas este Uriel José Esparza y en otra Omar Luna?
Solución: https://www.youtube.com/watch?v=bVfmSLrq7gc
5) Cuántas claves de acceso a una computadora será posible diseñar, si debe
constar de dos letras, seguidas de cinco dígitos, las letras serán tomadas del
abecedario y los números de entre los dígitos del 0 al 9. a. Considere que se
pueden repetir letras y números, b. Considere que no se pueden repetir letras y
números, c. ¿Cuántas de las claves del inciso b empiezan por la letra A y
terminan por el número 6?, d. ¿Cuántas de las claves del inciso b tienen la
letra R seguida de la L y terminan por un número impar?
Solución: https://studio.youtube.com/video/nEri4tNvOvs/edit
E) PERMUTACIONES CON
REPETICION.
En los casos anteriores se han obtenido
permutaciones en donde todos los elementos utilizados para hacer los arreglos son diferentes. A
continuación se obtendrá una fórmula que nos permite obtener las permutaciones de
n objetos, cuando entre esos objetos hay algunos que son iguales.
Ejemplo:
Obtenga todas las permutaciones posibles a
obtener con las letras de la palabra OSO.
Solución:
Para obtener la fórmula, es necesario primero
suponer que todas las letras de la palabra OSO son diferentes y para
diferenciarlas pondremos subíndices a las letras O, por lo que quedaría, O1SO2,
y las permutaciones a obtener serían:
3P3 = 3! =
6
definiendo las permutaciones tenemos que estas
serían,
O1SO2,
O2SO1, SO1O2, SO2O1,
O1O2S, O2O1S
¿Pero realmente podemos hacer diferentes a las
letras O?, eso no es posible, luego entonces ¿cuántos arreglos reales se
tienen?
Como:
Arreglos
reales
O1SO2
= O2SO1 ® OSO
SO1O2
= SO2O1 ® SOO
O1O2S=
O2O1S ® OOS
Entonces se observa que en realidad sólo es
posible obtener tres permutaciones con las letras de la palabra OSO debido a
que las letras O son idénticas, ¿pero qué es lo que nos hizo pensar en seis arreglos
en lugar de tres?, el cambio que hicimos entre las letras O cuando las
consideramos diferentes, cuando en realidad son iguales.
Para obtener los arreglos reales es necesario
partir de la siguiente expresión:
Los cambios entre objetos iguales
El número de arreglos reales = 3! /
2! = 3 x 2! / 2! = 3
Por tanto
la fórmula a utilizar sería;
nPx1,x2 ,........,xk
x1! x2 ... xk!
nPx1,x2,......, xk
= Número total de permutaciones que es posible obtener con n objetos, entre los
que hay una cantidad x1 de objetos de cierto tipo, una cantidad x2
de objetos de un segundo tipo,...... y una cantidad xk de objetos
del tipo k.
n = x1 + x2 + ...... + xk
Ejercicios:
1) Obtenga
todas las señales posibles que se pueden diseñar con seis banderines, dos de
los cuales son rojos, tres son verdes y uno morado.
2) a.¿Cuántas
claves de acceso a una computadora será posible diseñar con los números
1,1,1,2,3,3,3,3?, b.¿cuántas de las claves anteriores empiezan por un número
uno seguido de un dos?, c. ¿cuántas de las
claves del inciso a empiezan por el número dos y terminan por el número
tres?
Solución: https://www.youtube.com/watch?v=gRxttdLiaJI
3) ¿De
cuántas maneras es posible plantar en una línea divisoria de un terreno dos
nogales, cuatro manzanos y tres ciruelos?
Solución: https://www.youtube.com/watch?v=dE1kkIPOmRw
4) Si
un equipo de fútbol soccer femenil participa en 12 juegos en una temporada,
¿cuántas maneras hay de que entre esos doce juegos en que participa, obtenga 7
victorias, 3 empates y 2 juegos perdidos?
F)
PRUEBAS ORDENADAS.
Se le llama prueba
ordenada al hecho de seleccionar r objetos de entre n objetos
contenidos en una urna uno tras otro. Una prueba ordenada puede ser llevada a
efecto de dos maneras:
1) Con sustitución
(con reemplazo).- En este caso se procede a seleccionar el primer objeto de
entre los n que hay, se observa de qué tipo es y se procede a regresarlo
a la urna, luego se selecciona el siguiente objeto, lo anterior se repite hasta
que se han extraído los r objetos de la prueba, por tanto el número de
pruebas ordenadas de con sustitución se obtiene:
Número total de pruebas ordenadas con
sustitución = n x n x n x .........x n = nr
Hay n maneras de
seleccionar el primer objeto, luego al seleccionar el segundo objeto, dado que
se ha regresado a la urna el primer objeto, también se tendrán n objetos y así
sucesivamente.
2) Sin sustitución
(sin reemplazo).- En este caso se procede a seleccionar el primer objeto, el
cual no es regresado a la urna, luego se selecciona el segundo objeto, lo
anterior se repite hasta completar los r objetos de la prueba, por lo
que el número total de pruebas ordenadas sin sustitución se obtiene:
Número total de pruebas ordenadas sin sustitución = n(n-1)(n-2).........(n-r +1) = nPr
Hay n maneras de
seleccionar el primer objeto, luego al seleccionar el segundo objeto, hay n –1
maneras, dado que el primer objeto no se regresa a la urna, luego cuando se
extrae el r-ésimo objeto, hay (n –r +1) de que sea seleccionado.
1) ¿Cuántas maneras
hay de que se asignen tres premios de un sorteo en donde el primer premio es
una departamento, el segundo premio es un auto y el tercer premio es un centro
de cómputo, si los participantes en este sorteo son 120 personas, a.sí la
asignación se puede hacer con sustitución, b.sí la asignación se puede hacer
sin sustitución.
2) ¿Cuántas formas hay
de asignar las primeras cinco posiciones de una carrera de autos de fórmula K,
si participan 26 autos en esta carrera?. Considere que la asignación es
totalmente al azar.
3) ¿Cuántas formas hay
de asignar el orden de participación de las primeras 5 concursantes de 11
finalistas de un concurso de Miss Mundo?
G) COMBINACIONES.
Como ya se mencionó
anteriormente, una combinación, es un arreglo de elementos en donde no nos
interesa el lugar o posición que ocupan los mismos dentro del arreglo. En una
combinación nos interesa formar grupos y el contenido de los mismos.
La fórmula para determinar el
número de combinaciones es:
nCr = n!
(n - r) r!
Donde se observa que,
nCr = nPr
r!
La expresión anterior nos
explica como las combinaciones de r objetos tomados de entre n objetos pueden ser
obtenidas a partir de las permutaciones de r objetos tomados de entre n
objetos, esto se debe a que como en las combinaciones no nos importa el orden
de los objetos, entonces si tenemos las permutaciones de esos objetos al
dividirlas entre r!, les estamos quitando el orden y por tanto transformándolas
en combinaciones, de otra forma, también si deseamos calcular permutaciones y
tenemos las combinaciones, simplemente con multiplicar estas por el r!
obtendremos las permutaciones requeridas.
nPr
= nCr r!
Y si deseamos r = n entonces;
nCn
= n! / (n –n)!n! = n! / 0!n! = 1
¿Qué nos indica lo anterior?
Que cuando se desea formar
grupos con la misma cantidad de elementos con que se cuenta solo es posible
formar un grupo.
Ejercicios:
1) a. Si se cuenta con 14 alumnos que desean colaborar en una campaña pro
limpieza del Tec, cuantos grupos de limpieza podrán formarse si se desea que
consten de 5 alumnos cada uno de ellos, b.si entre los 14 alumnos hay 8
mujeres, ¿cuantos de los grupos de limpieza tendrán a 3 mujeres?, c.¿cuántos de
los grupos de limpieza contarán con 4 hombres por lo menos?
Solución: Serán Resueltos en Clase
2) Para contestar un examen un alumno debe contestar 9 de 12 preguntas, a. ¿Cuántas maneras tiene el
alumno de seleccionar las 9 preguntas?, b.¿Cuántas maneras tiene si
forzosamente debe contestar las 2
primeras preguntas?, c.¿Cuántas maneras tiene si debe contestar una de
las 3 primeras preguntas?, d.¿Cuántas maneras tiene si debe contestar como
máximo una de las 3 primeras preguntas?
Solución: Serán Resueltos en Clase
3) Una señora desea invitar a cenar a 5 de 11 amigos que tiene, a. ¿Cuántas
maneras tiene de invitarlos?, b. ¿cuántas maneras tiene si entre ellos está una
pareja de recién casados y no asisten el uno sin el otro, c. ¿Cuántas maneras
tiene de invitarlos si Rafael y Arturo no se llevan bien y no van juntos?
Solución: Serán Resueltos en Clase
H) PARTICIONES ORDENADAS.
Se le llama partición ordenada al hecho
de repartir n objetos en células de una cantidad de x1 objetos, x2 objetos,......y xk objetos.
Para deducir la fórmula de particiones
ordenadas partiremos de un ejemplo.
¿Cuántas maneras hay de repartir 10
libros diferentes entre tres alumnos, si al primero le daremos 2, al segundo 3
y el resto al tercer alumno?
Ejemplos de esta partición serían las
siguientes si se numeran los libros del 1 al 10;
Solución:
Lo primero que debemos hacer es
seleccionar 2 libros de los 10 que se tienen para el primer alumno, esto es;
10C2 =
10! / (10 – 2)!2! = 10! / 8!2! = 45 maneras de seleccionar los libros
Luego se seleccionan 3 libros de los 8
que quedan para el segundo alumno;
8C3 =
8! / (8 – 3)!3! = 8! / 5!3! = 56 maneras
Y por último se procederá a seleccionar
cinco libros de los cinco que quedan para el tercer alumno, lo que se muestra a
continuación;
5C5 =
5! / (5 –5)!5! = 5! / 0!5! = 1 manera
Por tanto el número total de
particiones ordenadas en células de 2, 3 y 5 elementos se determina:
10C2*8C3*5C5 =
(10! / (10 – 2)!2!)*(8! / (8 – 3)!3!)*(5! / (5 – 5)!5!) = 10! /2!3!5!
La expresión anterior nos recuerda a la
fórmula utilizada para encontrar las permutaciones de n objetos, entre los
cuales hay algunos objetos que son iguales, por lo que usaremos la misma
fórmula para encontrar las particiones ordenadas.
Por tanto la fórmula para las
particiones ordenadas sería:
Esta fórmula sólo puede ser utilizada
cuando se reparten todos los objetos, no parte de ellos, en ese caso se usarán
combinaciones.
Donde:
nPx1,x2,.....,xk =
Total de particiones ordenadas o reparticiones que es posible hacer cuando los n objetos
son repartidos en grupos de x1 objetos, x2 objetos
...... y xk objetos.
n
= x1 + x2 + ......+ xk
Ejercicios:
1) ¿Cuántas
maneras hay de repartir 9 juguetes entre tres niños, si se desea que al primer
niño le toquen 4 juguetes, al segundo 2 y al tercero 3 juguetes?
Solución: Serán Resueltos en Clase
2) ¿Cuántas
maneras hay de repartir los mismos 9 juguetes entre tres niños, si se desea
darle 3 al primer niño, 2 al segundo niño y 2 al tercer niño?
Solución: Serán Resueltos en Clase
3) a.
¿Cuántas maneras hay de que se repartan 14 libros diferentes entre 3 alumnos,
si se pretende que al primer alumno y al segundo les toquen 5 libros a cada uno
y al tercero le toque el resto?, b. ¿Cuántas maneras hay de que se repartan los
libros si se desea dar 5 libros al primer alumno, 3 al segundo y 2 libros al
tercer alumno?
Solución: Serán Resueltos en Clase
4) a.¿Cuántas
maneras hay de repartir a 12 alumnos en 4 equipos de 3 personas cada uno de
ellos para que realicen prácticas de laboratorio diferentes?, b.
¿Cuantas maneras hay de que se repartan los 12 alumnos en 4 equipos de 3
personas si se va a realizar una misma práctica?
Solución: Serán Resueltos en Clase
I. DIAGRAMA DE ARBOL.
Un diagrama
de árbol es una representación gráfica de un experimento que consta de r pasos,
donde cada uno de los pasos tiene un número finito de maneras de ser llevado a
cabo.
Ejemplo:
1. Un médico general clasifica a sus pacientes
de acuerdo a: su sexo (masculino o femenino), tipo de sangre (A, B, AB u O) y
en cuanto a la presión sanguínea (Normal, Alta o Baja). Mediante un diagrama de
árbol diga en cuantas clasificaciones pueden estar los pacientes de este
médico?
Solución:
Serán resueltos en Clase
1) Dos equipos denominados A y B se disputan la
final de un partido de baloncesto, aquel equipo que gane dos juegos seguidos o
complete un total de tres juegos ganados será el que gane el torneo. Mediante
un diagrama de árbol diga
de cuantas maneras puede ser ganado este torneo,
Solución:
Serán resueltos en Clase
2) Un hombre tiene tiempo de jugar ruleta cinco
veces como máximo, él empieza a jugar con un dólar, apuesta cada vez un dólar y
puede ganar o perder en cada juego un dólar, él se va a retirar de jugar si
pierde todo su dinero, si gana tres dólares (esto es si completa un total de
cuatro dólares) o si completa los cinco juegos, mediante un diagrama de árbol,
diga cuántas maneras hay de que se efectué el juego de este hombre.
Solución:
Serán resueltos en Clase
UNIDAD II. PROBABILIDAD
En ocasiones cuando se habla de probabilidad o
posibilidad de que un evento ocurra, se pierde la credibilidad acerca del
evento en cuestión, pero ¿es posible tener siempre la certeza total en todo
proyecto o actividad que se desea realizar?, es muy difícil tenerla, debido a
que el llevar a efecto un proyecto cualquiera por más simple que este sea, éste
está sujeto a una gran diversidad de factores que afectan su ocurrencia,
¿entonces que es lo más aconsejable para predecir su ocurrencia?, la probabilidad es
la que nos ayuda en estos casos, ya que basándose en estadísticas, podemos
cuantificar la posibilidad de ocurrencia de los eventos y por consiguiente
tomar una buena decisión basados en esta información.
A) CONCEPTO.
La probabilidad se encarga de evaluar todas
aquellas actividades en donde se tiene incertidumbre acerca de los resultados
que se pueden esperar, esto quiere decir que la probabilidad está
presente en casi en todas las actividades que se pretenda realizar, ejemplos:
-Cualquier proyecto de Ingeniería o de otras
áreas
-Competencias deportivas
-Juegos de azar, etc., etc.
¿Cómo podemos calcular probabilidades?
1. Haciendo uso de las estadísticas.
En este caso, se hace uso de la información
que se ha acumulado acerca del evento que nos interesa, y después de esto se
procede a calcular las probabilidades requeridas.
Ejemplo. Determine la probabilidad de que en
cierta línea de producción se manufacture un producto defectuoso, si se toma
como referencia que la producción de la última semana en esta línea fue de
1,500 productos, entre los que se encontraron 8 productos defectuosos.
p(producto defectuoso) = No de productos
defectuoso /Total de productos producidos en la semana
=
18 / 1500 = 0.012
Lo anterior nos indica que es muy probable que
1.2 productos de cada 100 que se manufacturen en esa línea serán defectuosos.
¿Porqué se utilizó para calcular las
probabilidades la información de la semana inmediata anterior?. Debido a que
esta refleja la situación que guarda actualmente la producción de la línea
mencionada.
2. Basándose en la experimentación. Hay casos
en los que después de repetir un número muy grande de veces un experimento, es
posible determinar las probabilidades de ocurrencia de algunos eventos, tales
como: La probabilidad de que aparezca águila al lanzar una moneda equilibrada,
la probabilidad de que aparezca el número 3 en un dado, etc., etc.
Ejemplos:
p(águila) =1/2 = 0.5
p(aparezca el número 3)= 1 / 6 = 0.1666
3. Asignando probabilidades. En este caso se
hace uso de las probabilidades obtenidas mediante estadísticas y la
experimentación y se asignan a los eventos previamente descritos y a partir de
ellas se determinan probabilidades de otros eventos.
A continuación se definen algunas cuestiones
implícitas en el cálculo de probabilidades.
a) Espacio muestral (d).- Es el conjunto de
todos los resultados posibles de un experimento. Es nuestro Universo.
Ejemplos:
1. Se lanza al aire un dado normal
(perfectamente equilibrado), enumere los posibles resultados de este
experimento.
d= {1,
2, 3, 4, 5, 6 }
2. Se lanza al aire dos veces una moneda
normal, defina su espacio muestral.
d = {AA,
AS, SA, SS}
b) Evento A.- El evento A es un subconjunto
del espacio muestral.
Ejemplos:
1. Sea A el evento de que aparezca un número
par en el lanzamiento de un dado, entonces;
A
= {2,4,6}
2. Sea B el evento de que aparezcan dos
águilas en tres lanzamientos de una moneda normal, entonces;
Como d = {AAA,
AAS, SAA, ASA, ASS, SAS, SSA, SSS}
Luego B = {AAS, SAA, ASA}
a) Sea f un evento que carece de
elementos.
f = { }
Como se observa los experimentos y eventos
probabilísticos se pueden expresar con la notación de conjuntos y a
continuación se enumeran algunas operaciones que es posible realizar con los
eventos.
1) AÈB Es
el evento que ocurre si y solo sí A ocurre o B ocurre o ambos ocurren.
 |
 |
||
|
|
|
|
|
|
2) AÇB Es el evento que ocurre sí y solo sí A y B ocurren a un
mismo tiempo.
 |
 |
||
3) Ac Es el complemento de A. Es el evento que
ocurre sí y solo sí A no ocurre.
 |
1) Se dice que A y B son eventos mutuamente
excluyentes o exclusivos si AÇB = f
 |
Ejemplo:
En un salón de clase hay 15 alumnos, 7 de los cuáles son de tercer
semestre, 5 son de cuarto semestre y 3 son de quinto semestre de la carrera de
Ingeniería Química, de los cuales 4, 2 y 1 respectivamente dominan el Inglés,
si se selecciona un alumno al azar de este grupo, a. ¿cuál es la probabilidad
de que el alumno seleccionado sea de quinto semestre?, b. ¿cuál es la
probabilidad de que sea de tercero o cuarto semestre?, c. ¿cuál es la
probabilidad de que el alumno seleccionado sea de tercer semestre y domine el
inglés?, d. ¿cuál es la probabilidad de que el alumno seleccionado no domine el
inglés?, e. Diga si los eventos T y Q son mutuamente excluyentes, diga si los
eventos Q e I son mutuamente excluyentes?
Solución:
Empezaremos por definir algunos eventos;
T = evento de que un alumno sea de tercer semestre
Cu = evento de que un alumno sea de cuarto semestre
Q = evento de que un alumno sea de quinto semestre
I =
evento de que un alumno domine el inglés
a. p(alumno seleccionado sea de quinto semestre)
= p(Q) = 3/15 = 0.2
b. p(alumno seleccionado sea de tercero o cuarto
semestre)= p(T ÈCu) =
= p( T) + p(Cu) = 7/15 + 5/15 = 12/15 = 0.8
c. p(alumno sea de tercer semestre y domine el
inglés) = p(T Ç I) = 4/15 = 0.26667
d. p(alumno seleccionado no domine el inglés) =
p(Ic ) = 8/15 = 0.53333
e. Los eventos T y Q son mutuamente excluyentes
dado que TÇQ = f
Los eventos Q e I no son eventos mutuamente excluyentes, ya que QÇI= {1}
Ya que hay un alumno que cumple con ambos eventos, es de quinto semestre
y domina el inglés.
UNIDAD
III. ESTADISTICA DESCRIPTIVA.
a) CONCEPTO.
¿Qué es la estadística descriptiva o para qué nos sirve?
Cuando necesitamos analizar un proceso
cualquiera, es necesario tomar una muestra de datos del proceso en cuestión y a
partir de los mismos obtener sus características tales como la media, la
mediana, la moda, la desviación estándar, el rango, etc., también es necesario
saber el tipo de distribución de probabilidad que tiene, así como también es
necesario visualizar de forma objetiva el comportamiento de los datos al ser
graficados de diversas formas, todo lo anterior es posible gracias a la
estadística descriptiva.
¿Qué es una muestra? Es una parte de los datos
del proceso que se desea analizar, la cuál debe de ser representativa del
proceso en cuanto al número de elementos que contiene y en cuanto a lo que está
ocurriendo en el proceso, esto último se logra tomando cada uno de los
elementos de la muestra de forma aleatoria o totalmente al azar; para
determinar el número de elementos idóneo en la muestra se hace uso de la inferencia
estadística, por el momento no nos ocuparemos de ello debido a que esto se ve
con detalle en cursos más avanzados de estadística.
b) TRATAMIENTO PARA DATOS NO AGRUPADOS.
¿A qué se refiere esto? Cuando la
muestra que se ha tomado de la población o proceso que se desea analizar, es
decir, tenemos menos de 20 elementos en la muestra, entonces estos datos son
analizados sin necesidad de formar clases con ellos y a esto es a lo que se le
llama tratamiento de datos no agrupados.
b1. Medidas de tendencia central. Se
les llama medidas de tendencia central a la media aritmética, la mediana, la
media geométrica, la moda, etc. debido a que al observar la distribución de los
datos, estas tienden a estar localizadas generalmente en su parte central. A
continuación definiremos algunas medidas de tendencia central y la forma de
calcular su valor.
1) Media aritmética (`x ). También se le conoce
como promedio ya que es el promedio de las lecturas o mediciones individuales
que se tienen en la muestra, se determina con la fórmula siguiente:
donde:
`x = media aritmética
xi = dato i
n = número de datos
en la muestra
Ejemplos:
- Se han tomado como muestra las medidas de seis
cables usados en un arnés para lavadora, las cuales son; 15.2 cm, 15.0,
15.1, 15.2, 15.1 y 15.0, determine su media aritmética.
Solución:
2. Se toman
varias muestras de cierto tipo de queso y se determina la cantidad de proteína
por cada 100 gramos de queso, encontrándose lo siguiente: 26.5 gramos, 24.8,
25.3, 30.5, 21.4, determine la
cantidad promedio de proteína encontrada en la muestra por cada 100 gramos de
queso que se elabora.
Solución: serán Resuelto en clase
3. Se hacen varias lecturas de una muestra
que contiene cobre, las lecturas se hacen en un espectrofotómetro de absorción
atómica y son la siguientes: 12.3%, 12.28, 12.27, 12.3, 12.24, 15.01, determine
la concentración promedio de Cu en la muestra.
Solución:
Si observamos las lecturas del
espectrofotómetro nos damos cuenta que el valor de 15.01% es un valor diferente
al de las lecturas anteriores, por lo que se descarta el valor ya que se
considera un valor atípico,
es decir un valor que es debido a circunstancias especiales, en este caso puede
ser que se deba al hecho de que se está descalibrando el aparato de absorción
atómica o simplemente que se ha equivocado el operador del aparato al tomar la
lectura, por lo que la media se debe calcular con las primeras cinco lecturas;
como se muestra a continuación:
Solución: serán resuelto en clase
4. Si deseamos
determinar la edad promedio de los estudiantes de una escuela de nivel superior
al iniciar sus estudios, suponga que se toman las edades de algunos de los
alumnos de cierta clase y estas son las que siguen: 20, 18, 18, 19, 18, 19, 35,
20, 18, 18, 19.
Solución:
Luego, la
media se determinará con solo 10 de las edades ya que es necesario descartar la
edad de 35 años, que es un dato atípico o un caso especial, por lo que;
Nota: Cuando
es necesario determinar aquellas medidas de tendencia central que hagan uso de
todos los datos de la muestra se recomienda descartar todos aquellos datos
atípicos que se encuentren en la muestra o muestras tomadas.
2) Media geométrica (G). Es la raíz en enésima
del producto de los valores de los elementos de la muestra, es usada
cuando los valores de los
datos de la muestra no son lineales, es decir que su valor depende de varios
factores a la vez, se determina de la siguiente forma:
Donde:
G = media geométrica
xi = dato i
n = número de
datos en la muestra
Ejemplos:
1. Las siguientes temperaturas han sido tomadas de un proceso químico, 13.4oC,
12.8, 11.9, 13.6, determine la temperatura promedio de este proceso.
Solución:
G =
2. Las siguientes temperaturas han sido tomadas de un proceso para fabricar
queso chihuahua, 21.4oC, 23.1, 20.2, 19.7, 21.0, determine la
temperatura promedio de este proceso.
Solución:
G =
3) Media aritmética ponderada ( xw ). Esta media se usa cuando el peso
que tiene cada uno de los datos de la muestra es diferente, se calcula de la
siguiente manera:
donde:
xw = media
aritmética ponderada
xi = dato i
wi = peso del
dato i
Ejemplo:
A continuación se mencionan las materias que Luis Pérez llevó en el
primer semestre de Ingeniería Química, el número de créditos y la calificación
obtenida;
MATERIA
|
NUMERO CREDITOS
|
CALIFICACIÓN
|
Metodología de la investigación
|
8
|
90.5
|
Matemáticas I
|
10
|
100.0
|
Programación
|
8
|
81.0
|
Química
|
10
|
78.0
|
Dibujo
|
4
|
100.0
|
Economía
|
8
|
84.0
|
Determine la calificación promedio que obtuvo Luis Pérez en su
primer semestre.
Solución:
= 724 + 1000 + 648 + 780 + 400 + 672 = 4224 = 88.0
48 48
Nota: Sí comparamos este promedio con el que se obtiene usando
simplemente la media aritmética, que es un 88.91, nos damos cuenta de que este
último es mayor, por no tomar en cuenta el peso o número de créditos que aporta
cada materia a la carrera que se estudia, el promedio de esta persona es menor
al de la media aritmética debido a que obtiene una calificación baja es Química
que es una de las materias que aporta más créditos.
4) Media armónica (H). La media armónica se
define como el recíproco del promedio de los recíprocos de cada uno de los
datos que se tienen en la muestra, y
se
determina de la siguiente manera:
Ejemplo:
Determine la media armónica de los siguientes datos, 3.1, 2.8, 2.84, 3.05, 3.09
Solución:
5) Mediana (xmed). La mediana es
aquel valor que se encuentra en la parte central de los datos que se tienen en
la muestra una vez que estos han sido ordenados según su valor o magnitud. Para
calcular la mediana se presentan dos casos:
a. Cuando el número de datos en la muestra es
impar.- En este caso después de ordenar los datos de la muestra en cuanto a su
magnitud, es decir de mayor a menor valor o de menor a mayor valor, se procede
a localizar aquel dato que se encuentra justo en el centro de los datos o en la
parte central de los
mismos, el valor de este dato será el que dé valor a la mediana.
Ejemplo:
Los siguientes datos son las
mediciones obtenidas de un circuito utilizado en un arnés de lavadora; se toman
como muestra siete circuitos y sus mediciones son: 11.3, 11.2, 11.5, 11.2,
11.2, 11.4, 11.5 cm.
Solución:
Ordenando los datos de menor a mayor valor;
11.2, 11.2, 11.2, 11.3,
11.4, 11.5, 11.5
Se observa que el dato 11.3 es el que queda en la parte central,
por lo que este es el que dará valor a la mediana; entonces,
xmed = 11.3 cm.
b. Cuando el número de datos en la muestra es
par.- En este caso después de ordenar los datos en cuanto a su magnitud,
observamos que en la parte central de los datos no se encuentra dato alguno, en
este caso, la mediana tomará el valor del promedio de dos datos; el que se
encuentra antes de la parte central y el que se encuentra después de la parte
central.
Ejemplo:
Los siguientes datos son las mediciones
obtenidas de un circuito utilizado en un arnés de lavadora; se toman como
muestra ocho circuitos y sus mediciones son: 11.3, 11.2, 11.5, 11.2, 11.2,
11.4, 11.5, 11.4 cm.
Solución:
Ordenando los datos de mayor a menor
valor,
11.5, 11.4, 11.4, 11.3, 11.2, 11.2, 11.2, 11,1 cm.
Se observa que en la parte central de
los datos no hay dato alguno por lo que la mediana se determina con el promedio
de los datos subrayados, entonces,
Nota: Es imprescindible para calcular el
valor de la mediana el que primero se ordenen los datos en cuanto a su
magnitud, ya que de no hacerlo, se incurriría en un grave error.
5) Moda (xmod). La
moda se define como aquel valor o valores que más se repiten o que tienen mayor frecuencia entre los
datos que se han obtenido en una muestra, la muestra de una población nos genera la distribución de los
datos una vez que estos se han graficado y en esta gráfica es posible observar
la moda o modas de la misma, es por esto que una distribución de datos puede
ser amodal (carece de moda), unimodal (tiene una sola moda), bimodal (tiene dos
modas) o polimodal (tiene más de dos modas).
Ejemplos:
1. Determine la moda de los datos que se muestran a continuación, se
refieren a la estatura de un grupo de jóvenes; 1.60m, 1.65, 1.70, 1.71, 1.70,
1.70, 1.70, 1.71, 1.70, 1.93, 1.87, 1.85
Solución:
Estatura
|
Frecuencia
|
1.60
|
1
|
1.65
|
1
|
1.70
|
5*
|
1.71
|
2
|
1.85
|
1
|
1.87
|
1
|
1.93
|
1
|
La tabla muestra la distribución de frecuencias de los datos o el número
de veces que estos se repiten, la mayor frecuencia que es 5 corresponde a una
estatura de 1.70m, por lo que esta sería la moda.
Luego, xmod =
1.70m
2. Determine la moda de los siguientes datos que
se refieren a la edad de alumnos de primer semestre del tecnológico de
Chihuahua, 18 años, 17, 19, 21, 19, 18, 22, 22, 18, 18, 17, 19, 19, 19, 18, 20,
21, 20, 18, 19, 18, 19, 18,19, 22, 35
Solución:
Edad
|
Frecuencia
|
17
|
2
|
18
|
7*
|
19
|
8*
|
20
|
2
|
21
|
2
|
22
|
3
|
35
|
1
|
En este caso se observa que las edades que más frecuencia tienen son las
de 18 y 19 años, por lo que se concluye que existen dos modas,
Xmod1= 18 años , Xmod2= 19años
Hay que hacer notar que la frecuencia para ambas modas puede ser de igual
magnitud o diferente, como en el caso que se ilustra.
b2. Medidas de Dispersión. Cuando se tiene una muestra de datos obtenida
de una población cualquiera, es importante determinar sus medidas de tendencia
central así como también es básico el determinar que tan dispersos están los
datos en la muestra, por lo que se hace necesario determinar su rango, la
varianza, la desviación estándar, etc., ya que una excesiva variabilidad o
dispersión en los datos indica la inestabilidad del proceso en análisis en la
mayoría de los casos.
1) Rango o recorrido. El rango es la diferencia
entre el valor mayor y el valor menor encontrados en la muestra, también se le
denomina recorrido ya que nos dice entre que valores hace su recorrido la
variable de interés; y se determina de la siguiente manera:
R = VM – Vm
Donde:
R = rango o recorrido
VM = valor mayor
en la muestra
Vm = valor menor
en la muestra
Ejemplo:
1. Se han tomado como muestras las
mediciones de la resistencia a la tensión de la soldadura usada para unir dos
cables, estas son: 78.5kg, 82.4, 87.3, 78.0, 90.0, 86.5, 77.9, 92.4, 75.9,
determine su rango o recorrido.
Solución:
VM = 92.4 kg
Vm = 75.9 kg
R = VM – Vm = 92.4 – 75.9 = 16.5 kg
2. Se toman las mediciones de la
cantidad de grasa de la leche en gramos por cada 100 ml de leche que entra a un
proceso de pasteurización, a continuación se enumeran; 14.85, 15.32, 12.76,
16.29, 15.84, 17.3, 17.61, 16.33, determine el rango o recorrido de la cantidad
de grasa de la leche.
Solución:
VM = 17.61
Vm = 12.76
R = 17.61 – 12.76 = 4.85gramos
2) Desviación absoluta media (d ). Esta medida de dispersión nos representa la diferencia absoluta
promedio que existe entre cada dato que se encuentra en la muestra y la media
de los datos y se determina de la siguiente manera:
Donde:
xi = dato i
_
x = media aritmética de la muestra
n = número de datos en la muestra
Ejemplo:
1. Determine la desviación absoluta
media de los siguientes datos que son las concentraciones de plomo de algunas
muestras, las que a continuación se enumeran: 18gr, 12, 21, 19, 16, 20, 22
Solución:
Para determinar la desviación absoluta
media o promedio, lo primero que hay que hacer es calcular la media aritmética
de los datos de la muestra, la que es 128/7 =18.286, luego se procede a
calcular el promedio de las diferencias absolutas entre cada dato y la media
calculada.
La interpretación de este resultado
sería que el grado de alejamiento absoluto promedio de los datos con respecto a
su media es de 2.5305 gramos.
¿Por qué sacar el valor absoluto de las
diferencias entre cada dato y la media aritmética? Si solo se hicieran
diferencias entre cada dato y la media aritmética, estas tendrían signos
positivos y negativos ya que algunos datos son menores que la media y otros son
mayores que la media, luego al sumar las diferencias, con sus signos
correspondientes, éstas se irían anulando
unas con otras y no sería posible medir leal grado de alejamiento promedio de
los datos en la muestra.